Linkedin Facebook Instagram Youtube

Enhancing Structural Analysis Accuracy with Geometry-Based Adaptivity in FEA

Finite Element Analysis

Finite Element Analysis (FEA) is a powerful numerical method used to solve complex engineering problems involving intricate geometries, varying loading conditions, and boundary constraints. In FEA, a continuous domain is discretized into smaller finite elements, a process known as meshing. The accuracy of simulation results largely depends on how well the mesh captures the geometric features and maintains element quality.

To accurately represent fine details, engineers often use high-quality or fine mesh, but this comes at the cost of increased computational time and resource consumption. Complex geometries are particularly challenging to mesh with standard settings, often leading to compromised quality or excessive element count.

To address these challenges, Geometry-Based Adaptivity in FEA provides an efficient way to automatically refine the mesh during solving, ensuring optimal accuracy while minimizing computational costs. This feature intelligently adjusts the mesh to better capture topological details without requiring excessive manual intervention.

Understanding Adaptivity in FEA

Adaptivity in FEA involves dynamic mesh refinement during the solution process to improve accuracy. It uses an iterative feedback mechanism that updates internal mesh parameters either discretely or continuously, ensuring convergence and precision.

There are two primary adaptivity techniques:
  • 1. Nonlinear Adaptive Region
  • 2. Geometry-Based Adaptivity

1. Nonlinear Adaptive Region

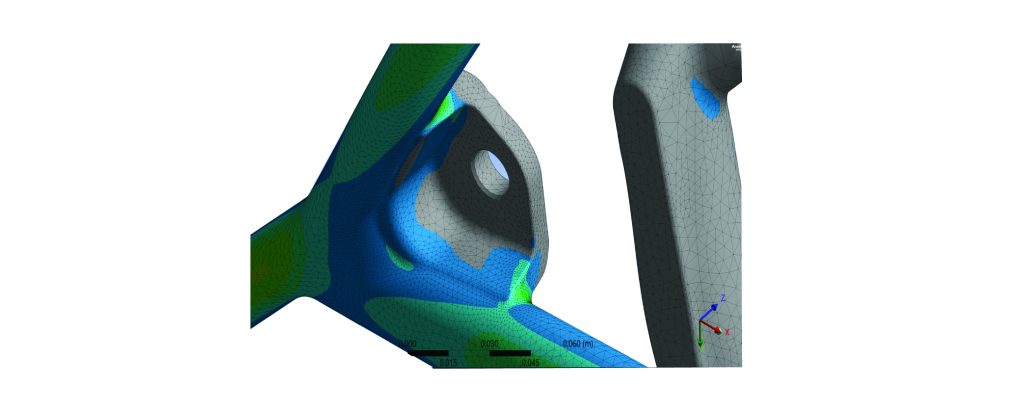
This technique helps reduce convergence issues in nonlinear analyses caused by element distortion. It remeshes the model based on initial mesh boundaries, meaning that a fine mesh is required from the start to capture geometric details.

2. Geometry-Based Adaptivity

Unlike the Nonlinear Adaptive Region, which remeshes within the initial mesh structure, Geometry-Based Adaptivity creates new nodes and elements along the actual geometry boundaries. This eliminates the need for an initial fine mesh, significantly reducing computational overhead while improving accuracy.

3. Key Benefits of Geometry-Based Adaptivity

  • Automatic Mesh Refinement: No manual intervention needed during solving.
  • Enhanced Accuracy: Captures geometric features dynamically without predefining a dense mesh.
  • Optimized Computational Resources: Reduces element count while maintaining precision.
  • Improved Efficiency: Helps analyze complex geometries without excessive computation time.
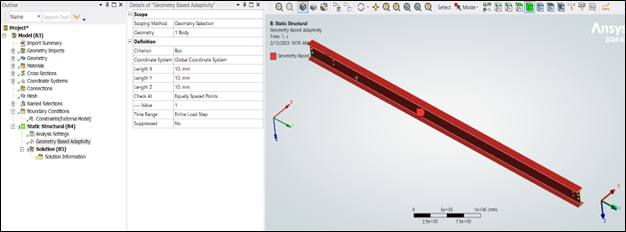
Finite Element Analysis

Fig. 1 Geometry Based Adaptivity in Ansys Mechanical

Requirements and Criterion

Geometry preserving adaptivity will be applicable to all the static analysis with Geometric nonlinearity turned off. This condition supports linear and quadratic tetrahedral elements. An assembly that includes both linear and quadratic elements cannot be used. Two criterions will be applicable to geometry preserving adaptivity, Energy and Box.

1. Energy Criterion

This criterion checks the strain energy of elements considered for this criterion and compares with mean strain energy of the component to which this element belongs. Mesh refinement will take place only when this criterion will be satisfied at a particular element. This criterion applied to areas having high stress concentration and elements are too large to attain high-accuracy simulation. Strain energy for each element is calculated and criterion will be checked using following equation.

Ee≥c1*ETotal/NUME

Where:
  • Ee = strain energy of single target element
  • c1 = user input energy coefficient
  • ETotal = total strain energy of the component
  • NUME = number of elements of the component
If this criterion is satisfied at an element, the program refines the element. A smaller Energy Coefficient improves the potential to trigger the mesh regeneration for the same loads.

2. Box Criterion

This criterion is based on user defined box creation; a region is defined in the global or local coordinates. If all nodes of an element are within the user defined region, the element is either refined via general remeshing or it is split based upon element type. If Box is selected, the following additional properties require entries:
  • Coordinate System (default is Global Coordinate System): defines the minimum values of the box.
  • Length X: defines the diagonal length on global X axis.
  • Length Y: defines the diagonal length on global Y axis.
  • Length Z (for 3D): defines the diagonal length on global Z axis.
This method is particularly useful when targeting specific regions for refinement instead of refining the entire model.

Fig. 2 Geometry based adaptivity utilization

Conclusion

Optimizing mesh accuracy and computational efficiency is a fundamental challenge in FEA. Geometry-Based Adaptivity presents a game-changing solution by dynamically refining the mesh only where needed, eliminating the need for excessive manual intervention.

By automatically adjusting element density based on energy concentration and geometric features, this approach ensures that simulations are both accurate and computationally efficient. As industries continue to push the limits of engineering complexity, Geometry-Based Adaptivity will remain a crucial tool for achieving high-fidelity simulations without excessive computational costs.

© Copyright 2025 by CADFEM APAC

Legal Notices

Privacy Policy

Terms of Use

Cookie Policy

Export Control Regulations

Terms and Conditions

Site Map